En las dos sesiones —la de jóvenes y la de adultos— del Club de Lectura del pasado miércoles, 18 de septiembre de 2013, comentamos el libro La fórmula preferida del profesor, de la escritora japonesa Yoko Ogawa (Okayama, Japón, 1962). En la portada del libro ya podemos descubrir, de hecho, cuál es esa fórmula, la que está escribiendo un niño en la pizarra, la llamada identidad de Euler, un caso especial de la fórmula que desarrolló el matemático Leonhard Euler:
 Cuando el otro día, antes de haberle hablado de este libro en particular, me encontré con Jesús Villagrá, profesor jubilado de matemáticas en nuestro instituto, y le pregunté cuál era su fórmula matemática favorita, me contestó que la identidad de Euler, y esa preferencia, según parece, es bastante generalizada entre los expertos… Pues bien, ¿qué tiene esa fórmula para que sea la preferida por tantos matemáticos?
Cuando el otro día, antes de haberle hablado de este libro en particular, me encontré con Jesús Villagrá, profesor jubilado de matemáticas en nuestro instituto, y le pregunté cuál era su fórmula matemática favorita, me contestó que la identidad de Euler, y esa preferencia, según parece, es bastante generalizada entre los expertos… Pues bien, ¿qué tiene esa fórmula para que sea la preferida por tantos matemáticos?
Ya sabemos que las matemáticas no todos las viven igual; a algunos alumnos, por ejemplo, se les atragantan y les parece que no van a poder superarlas nunca; para otros, en cambio, las matemáticas son una de las bases más sólidas para adentrarse en el conocimiento y en la belleza, quizá incluso la base más rigurosa para conocer la arquitectura invisible del universo. Precisamente por eso, el profesor Jesús Villagrá aludía brillantemente a esa desigualdad con el ingenioso título de uno de sus libros divulgativos, ¿Matemágicas o matetrágicas? Claves matemáticas para lectores inexpertos (Ediciones de Intervención Cultural, Barcelona, 2004), “un viaje —sin angustias ni agobios— a través de algunos conceptos del álgebra y del cálculo infinitesimal”.
Pero que nadie se asuste, porque lo cierto es que para leer y comentar la novela de Yoko Ogawa no se requieren grandes conocimientos de matemáticas; de la novela se han vendido millones de ejemplares en todo el mundo (sobre todo en Japón) y la mayor parte de sus lectores no eran expertos en matemáticas ni mucho menos. Es verdad que a lo largo de la historia que cuenta se mencionan conceptos matemáticos (números primos, números amigos, números naturales, números imaginarios, etc.), pero algunos de esos conceptos están explicados de una manera cordial, imaginativa y gozosa que lleva al lector a descubrirlos o a redescubrirlos con otros ojos, como si fueran —que lo son— una maravilla camuflada. Por ejemplo, cuando el profesor protagonista habla de la raíz cuadrada de -1, dice que “es un número muy discreto, no se muestra en público, pero está ahí dentro del corazón y sostiene el mundo con sus pequeñas manos”. Con un lenguaje tan cálido, ¿quién no se sentirá atraído por la raíz cuadrada de menos 1? Hablemos, pues, de la novela.
La narradora nos cuenta su experiencia como asistenta en la casa de un profesor de matemáticas que por una lesión cerebral —consecuencia de un accidente de tráfico— ha perdido casi prácticamente la memoria (los recuerdos se le borran enseguida; sólo le duran 80 minutos). La mujer, madre soltera de un niño de diez años (ella tiene unos treinta; el profesor, 64), ha sido contratada a través de una agencia para limpiar, lavar y cocinar para el profesor, quien no sale a la calle y vive recluido en un pabellón anexo a la casa en la que reside su cuñada, viuda de su hermano. Cuando el profesor conoce al hijo de su asistenta empieza a llamarlo Root (raíz cuadrada), pues la cabeza plana del niño le recuerda el signo de la raíz cuadrada. (Recuérdese que el símbolo de la raíz cuadrada representa la r de radix, palabra latina que significa raíz, pero con el trazo horizontal alargado como si fuera un brazo bajo el que se protegen los números.) A partir de entonces, el profesor, su asistenta y el niño componen una singular familia unida por fuertes vínculos de amistad y cariño en torno a las matemáticas y al béisbol, otra pasión que comparten el niño y el profesor. El nudo de la historia se localiza en el momento en que la cuñada acusa injustificada y cruelmente a la asistenta delante del niño y del profesor. Si hay algo que el profesor no puede soportar es que alguien pueda hacer daño o maltratar psicológicamente a un niño, por eso, incapaz de desarrollar verbalmente su opinión o de describir con exactitud su estado de ánimo, a punto de estallar de rabia viendo el sufrimiento que está viviendo Root (“¡No, no es posible! ¡No es tolerable herir los sentimientos de un niño”), recurre a una defensa infalible: escribe en un papelito su fórmula preferida, la identidad de Euler, la pone sobre la mesa ante los ojos de su cuñada y se marcha de la habitación.
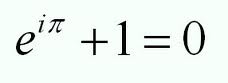 Y desde ese día la asistenta, que había abandonado los estudios de bachillerato cuando quedó embarazada y que sólo tiene nociones básicas de matemáticas, empieza una fascinante investigación en la biblioteca para averiguar qué había querido decir el profesor al utilizar esa fórmula como arma dialéctica para zanjar la discusión. Y en su investigación averigua cuál fue el último teorema de Fermat y, poco después, por qué la fórmula de Eiler es la preferida por tantos matemáticos: porque esa fórmula aglutina de manera muy elegante, además del 0 y el 1, “los números más interesantes en la disciplina, como el número e, base del crecimiento; el número π, que relaciona la longitud de una circunferencia con su radio; y la unidad imaginaria i, que da lugar a los números complejos, todos ellos reunidos en la fantástica relación e^(iπ) + 1 = 0” (Manuel de León, director del Instituto de Ciencias Matemáticas).
Y desde ese día la asistenta, que había abandonado los estudios de bachillerato cuando quedó embarazada y que sólo tiene nociones básicas de matemáticas, empieza una fascinante investigación en la biblioteca para averiguar qué había querido decir el profesor al utilizar esa fórmula como arma dialéctica para zanjar la discusión. Y en su investigación averigua cuál fue el último teorema de Fermat y, poco después, por qué la fórmula de Eiler es la preferida por tantos matemáticos: porque esa fórmula aglutina de manera muy elegante, además del 0 y el 1, “los números más interesantes en la disciplina, como el número e, base del crecimiento; el número π, que relaciona la longitud de una circunferencia con su radio; y la unidad imaginaria i, que da lugar a los números complejos, todos ellos reunidos en la fantástica relación e^(iπ) + 1 = 0” (Manuel de León, director del Instituto de Ciencias Matemáticas).
La verdad esencial que trata de transmitir esta novela se puede expresar de muchas maneras, por supuesto. Una de ellas sería diciendo que la belleza de las matemáticas puede oponerse con éxito a las barbaridades que, a veces, protagonizan los seres humanos. Es decir, la fuerza de la ternura que le inspira el niño al profesor le lleva a éste a tratar de protegerlo y a sintetizar con una hermosa fórmula matemática su rechazo de la maldad y de la injusticia que está representando la cuñada en un determinado momento. Pero, naturalmente, puede haber otras interpretaciones de la novela, como puede haber quienes prefieran otras fórmulas matemáticas. Por eso dejamos esto aquí, sin comentar el desenlace de la historia ni añadir ningún otro detalle más: para que cada lector de este blog que lo desee pueda exponer su opinión sobre el libro en general o sobre alguno de los cuatro personajes en particular, o pueda, al menos, decir cuál es su fórmula matemática preferida y por qué.

Efectivamente en la novela hay matemáticas pero estas no se convierten nunca en matetrágicas. Se cuenta el tiempo que compartieron unos personajes buenos y desvalidos, cada uno a su manera, y cómo formaron una familia.
Claro que uno de ellos es matemático y eso, además de su dolencia, contribuye a crear una barrera entre él y la mayoría. Pero esa barrera se deshace ante las personas adecuadas, mostrando a una persona de muy buena pasta que quiere mucho a los niños.
El profesor vive en su mundo, resuelve problemas que aparecen en revistas matemáticas con bellas demostraciones e ignora los premios que recibe. Para mí el profesor es un Hacker que encarna la ética hacker.
Y me recuerda mucho a un matemático de carne y hueso, a Grigori Perelman (Григо́рий Я́ковлевич Перельма́н), que también puede ser un magnífico ejemplo de Hacker.
Grigori se ha apartado del mundo y vive en un piso con su madre. Sus trabajos le llevaron a merecer la medalla Fields (que es el premio más prestigioso en las Matemáticas) pero lo rechazó diciendo que el premio “era completamente irrelevante para mí. Todo el mundo entiende que, si la demostración es correcta, entonces no se necesita ningún otro reconocimiento”.
También ganó uno de los premios del milenio que el Clay Mathematics Institute dota con 1 millón de dólares al demostrar la Conjetura de Poincaré. Premio que también rechazó.
Parte de su distanciamiento hacia ciertas instituciones se debe a la actitud que tuvieron algunos matemáticos al revisar su trabajo. Perelman considera que no fue ética ni aceptable la actitud de Shing-Tung Yau y, sobre todo, que el resto de la comunidad matemática guardase silencio.
En palabras de Perelman: “no puedo decir que estoy indignado. Otras personas hacen cosas peores. Por supuesto, hay muchos matemáticos que son más o menos honestos. Pero de ellos, casi todos son conformistas. Son más o menos honestos, pero toleran a quienes no son honestos”. El matemático no parece un ingenuo que haya descubierto la estafa por primera vez en la vida, es solo que en lo relativo a las matemáticas no lo puede soportar. Y para él las matemáticas son un refugio vital, como para el profesor.
Volviendo a la novela, que está escrita en un tono muy tranquilo y sutil, deja percibir la dureza de la sociedad japonesa. Que ciertamente tiene cualidades admirables que no necesito enumerar, pero la protagonista claramente tiene un trabajo precario que le impide atender a su hijo. El profesor no parece contar con ningún tipo de pensión para su subsistencia y pagar una pequeña cura ambulatoria en la que al niño le ponen 2 puntos en un corte supone un problema para su madre. Triste.
Se me ha olvidado contestar a la pregunta sobre la fórmula favorita… la verdad es que dudo tener alguna fórmula matemática favorita. Es verdad que en primero de carrera, el profesor de cálculo, como buen matemático, nos dijo que la identidad de Euler era la suya.
Por no redundar, y porque siempre que la tuve que utilizar me parecía una fórmula mágica, yo voy a decir la Transformada de Fourier (http://es.wikipedia.org/wiki/Transformada_de_fourier#Definici.C3.B3n). En este caso el aspecto caligráfico puede no ser tan elegante, es más complejo. Pero su función de puerta entre dos dominios siempre me ha parecido mágica.
Hola.
No tengo ninguna fórmula preferida, la verdad. Siempre las he visto como un mero instrumento para interpretar la realidad (bueno, un modelo de la realidad), aunque no hay duda de que muchas gozan de una belleza casi mística.
Si tengo que destacar alguna, me quedo con las series (http://en.wikipedia.org/wiki/List_of_mathematical_series). Me fascina pensar que un conjunto (finito o no) de valores pueda dar resultados tan exactos y espectaculares como, por ejemplo, la función zeta de Riemann (ya me dirán, por ejemplo para n=2, qué tiene que ver la razón entre la longitud de una circunferencia y su diámetro —es decir, pi— con la suma de fracciones 1/k^2) o la serie harmónica alternada, que da como resultado ln(2) (¡¿por qué?!), o las múltiples series de Taylor cuyos elementos funcionan como perfectos ladrillos de una construcción perfecta…
Otro tema apasionante es el de la geometría. Me parece genial que figuras y dibujos se puedan expresar con simples letras y números. Decir que x^2 + y^2= 1 es una circunferencia y que además tiene un tamaño y ubicación perfectamente sabidos me parece algo brutal. Y si a eso ya le juntamos la trigonometría, ¡la de relaciones insospechadas que empiezan a salir!
En fin, que éste es un tema inabarcable.
Leí el libro hace tiempo por recomendación de un gran amante de las matemáticas. Lo empecé a leer con cierto recelo puesto que las matemáticas y yo siempre hemos mantenido una relación no más allá de la cordialidad, pero lo cierto es que el objetivo del libro no es enseñar matemáticas.
Meses después, cuando se propuso como lectura en el Club, sólo guardaba de él las sensaciones que me provocó. Recordaba la calidez de los personajes cuando se trataban entre ellos, la ternura del Profesor hacia los niños, la admiración hacia el Profesor por cómo enseñaba sin proponérselo, el respeto entre los personajes…
¿Cómo es posible que no recordase el libro habiéndolo leído pocos meses antes y habiéndome dejado tan buenas sensaciones? Como me comentó uno de los tertulianos y gran amigo, me pasa como al Profesor, él olvida su vida cada 80 minutos, yo olvido un libro, aproximadamente, cada 60x24x30 minutos, así que antes de que me vuelva a olvidar, lo simplificaré diciendo que el libro muestra cómo cada uno de los personajes aporta lo que puede de sí mismo: cariño, celos, juventud, impaciencia, sabiduría, olvido…y así logra que los demás se sientan felices y acaben sintiendo que forman parte de una misma familia.
Dado el reto de tener que elegir mi fórmula favorita, diré que teniendo en cuenta mi relación con las matemáticas no soy capaz de ofrecer mucho, ahora bien, siempre ha habido dos ideas o conceptos que me han fascinado.
Uno es la existencia de infinitos números. Es un concepto asombroso si pensamos en él. Saber que podemos estar contando durante toda nuestra vida y que jamás existirá un límite es hermoso. ¡Es más! Podríamos dejarles a nuestros hijos, como herencia, el último número que pronunciemos justo antes de morir y ellos podrían seguir contando también hasta el fin de sus días. ¡Infinito! Una palabra que intenta englobar el concepto infinito. ¡Intentar englobar el infinito es imposible!
La otra idea que me atrae es la Sucesión de Fibonacci, otra maravilla, 0 1 1 2 3 5 8 13… y así hasta el infinito. Su fórmula es fn = f{n-1} + f{n-2} teniendo en cuenta que f{0}=0 y f{1}=1. Dicho de otra manera, para obtener un número de la sucesión hemos de sumar los dos anteriores, teniendo en cuenta que el primer número de la sucesión siempre es 0 y el segundo siempre es 1. Al principio los números apenas distan el uno del otro, pero a medida que la sucesión avanza, los números se alejan más del anterior. Además, podemos encontrar esta sucesión en la Naturaleza de manera recurrente.
Recuerdo que hace años, cuando reformaron la zona del puerto, hicieron un paseo precioso e incrustado en el suelo pusieron pequeñas claraboyas que en su interior, con fluorescentes de colores, aparecían números. Hoy en día ya no están.
Las primeras claraboyas estaban situadas una al lado de la otra, casi, casi, tocándose, y poco a poco se alejaban, la distancia entre ellas iba aumentando. ¿Sabéis qué números había en su interior? En la primera claraboya había un 0, en la segunda un 1, en la tercera otro 1… Sí, lo habéis adivinado: 0 1 1 2 3 5 8 13 21… Cuando descubrí qué era, me pasé un rato saltando de claraboya en claraboya mientras explicaba en voz alta la sucesión. Salto a la primera claraboya. Cero. Salto a la segunda claraboya. Uno. Salto a la tercera claraboya. Uno. Salto a la segunda claraboya, salto a la tercera y salto a la cuarta. Uno y uno, dos…
La divulgación de las matemáticas a través de novelas como esta es un gran recurso para introducir una visión positiva de la ciencia perfecta, para aquellos que tenemos una relación tensa con la susodicha. Y… efectivamente, nunca me habían parecido tan cálidas. Tan llenas de vida y pasión. Nunca me habían parecido tan inmensamente artísticas. Y es que la visión de Ogawa evocada en el entrañable personaje del Profesor es precisamente eso; puro arte. Conceptos a menudo distanciados el uno del otro, ciencia y arte.
Así pues, en lo personal me ha conmovido especialmente esa atmósfera que se crea entre los tres personajes principales, porque representa un valor que considero esencial para nuestra existencia armoniosa y pacifica:
Todos esos espacios de la vida en los que estamos aprendiendo de los demás, esos espacios en los que la sabiduría flota en el aire y se posa de manera casi imperceptible sobre nuestras cabezas, son lugares sencillamente mágicos.
Sí, este libro representa, entre muchas otras cosas, el valor del aprendizaje. El valor de la humildad, de la dedicación y del servicio. Especialmente también el valor del amor.
Una vez más, una profunda historia nos cuenta cómo todo es posible a través del amor. Porque esos segundos que han removido nuestros corazones mientras podíamos leer la felicidad, la satisfacción, el respeto o la tolerancia, nos recuerdan que sin importar los inhóspitos entornos grises en los que vivimos, en nuestro interior un corazón está latiendo, y con él podemos cambiar nuestro mundo.
Bueno, qué decir después de los comentarios que me preceden…
Realmente, es un libro que de entrada te resulta enigmático, porque no piensas qué puede resultar de una historia cuyo tema principal son las matemáticas.
Pero cuando te adentras en la historia, realmente te atrapa, porque es una historia que se basa en la relación que mantienen fundamentalmente los tres personajes que componen esta historia. Una relación marcada por un profesor de matemáticas que tiene muchas peculiaridades y limitaciones en su comportamiento, debido al accidente que sufrió. Pero que hace que se cree una relación de respeto y cariño profundo, en la que la matemáticas juegan de forma estratégica con el desarrollo de sus vidas, las cuales se ven impregnadas de ellas sin quererlo y marcan su futuro.
Es un libro que te hace ver el otro lado de la matemáticas, de relaciones entre números que no conocías y que te aportan otra visión de los conceptos básicos de la misma.
También aporta una dosis de amor romántico… que hay que descubrir.
La amistad, la honestidad, el respeto… valores importantes que se manejan en esta novela que llevan a la reflexión… y te dejan una sensación muy positiva después de leer el libro.
Después de leer con atención tanto la entrada del blog como los comentarios, todos ellos muy interesantes, me gustaría comentar dos aspectos del libro que me parecen importantes y que se pueden considerar como dos pasiones fundamentales para el profesor: la educación y el béisbol.
(Lógicamente la pasión principal para el profesor son las matemáticas, pero es un tema del que no puedo comentar nada interesante después de leer algunos de los comentarios anteriores.)
De la educación destaca la pasión con la que el profesor enseña sus extraordinarios conocimientos matemáticos. De las lecciones del profesor se dice que una “cosa extraña era que él utilizaba sin ningún problema la frase ‘no se sabe’. No era una vergüenza el no saber, sino sólo una señal que podía llevar hacia una nueva verdad”. Nunca hemos de sentir vergüenza por no saber, sino que esa conciencia ha de servirnos siempre, a lo largo de toda la vida, para adquirir nuevos conocimientos. También es muy bonita la relación entre el profesor y el niño, cada vez más estrecha y emotiva, pero para que sea así hay un elemento esencial que sirve de nexo de unión entre ambos personajes: el béisbol.
Aunque el béisbol en particular, y el deporte en general, no goce de muchas simpatías ni de mucha consideración en ciertos ámbitos culturales, es innegable que es uno de los espectáculos actuales que más desata pasiones entre público muy variado, de sectores sociales y culturales muy diferentes. Porque eso es lo que importa en el libro: destacar que la vida de cada uno adquiere sentido gracias a nuestras pasiones cotidianas, ésas que podemos cultivar, desarrollar y compartir cada día y que nos acompañan durante toda la vida, las que nos hacen seguir sintiéndonos vivos, a pesar de los problemas, pequeños y grandes, que siempre nos acompañan. Todo se puede superar para seguir viviendo, incluso una autonomía de la memoria de sólo ochenta minutos, como la del extraordinario profesor de este libro.
Solamente puedo decir que me ha encantado el libro. Totalmente aconsejable tanto para los amantes de las matemáticas como a los que no les gusta tanto.
Es un libro que te hace pensar y reflexionar, muy interesante.
La verdad es que no he leído el libro, pero al abrir este blog he ido rápidamente a esta entrada, supongo que he tenido curiosidad por conocer opiniones sobre la fórmula matemática preferida.
La verdad es que no me había parado nunca a pensar cuál es mi fórmula preferida. Lo que siempre me ha fascinado de este campo es ver cómo desde pequeños nos han enseñado las cosas más esenciales de las matemáticas y cómo poco a poco vas adentrándote en ellas y vas viendo cosas más complejas. Pero al final todo se reduce a lo básico, pero de una manera más fácil y rápida de hacer.
También me fascina ver cómo todo lo que nos rodea puede ser reducido a la matemática. Pero si tengo que decidirme por una fórmula, supongo que me decidiría por la fórmula que llevamos usando desde 2º de ESO para resolver ecuaciones de segundo grado.
Yo no me he leído el libro, pero al leer estos comentarios dan ganas de ir a la biblioteca, coger el libro y leerlo. El tema de las matemáticas es muy interesante, es un tema de interés universal: todos deberían tener conocimientos matemáticos, pues cada día usamos las matemáticas aunque no nos demos cuenta. Yo, por ahora, no tengo una fórmula preferida, seguramente en un futuro próximo la tendré, pero ahora no. Lo que me interesa es el tema de las fórmulas no demostradas todavía, como algunas que podemos encontrar en la redes. Hay una organización que ofrece una recompensa de un millón de euros por resolver unas fórmulas no demostradas, razonando el proceso en el que se realiza y matemáticamente (como hacemos normalmente en las clases de matemáticas, con mucha lógica), hasta te pueden dar el equivalente al premio Nobel por resolver uno de estos ejercicios. Estos problemas los podemos encontrar en Google, problemas del milenio, son 7 en total, y por ahora solo 1 está demostrado. Lo impresionante es que se tardó un siglo en encontrar la demostración y el matemático que la resolvió tardó, según algunos de los espectadores que lo vieron resolverla, 2 horas y 10 minutos. Las matemáticas incluso en esta época tan tecnológica y lógica siguen teniendo misterios sin resolver, son muy interesantes estos problemas, te hacen mover el cerebro al primer instante en el que los lees, y no es nada fácil descubrir lo que plantean.
¿Por qué el profesor compara las matemáticas con las estrellas?